CONTINUIDAD DE FUNCION

--------------------------------------------------------------------------------------------------------------------------------

En matemáticas, la continuidad de una función es una propiedad fundamental que describe cómo se comporta la función en relación con los valores cercanos de su dominio. Así, una función se considera continua si no presenta saltos, puntos indefinidos o discontinuidades en su gráfica.

Más formalmente, una función f(x) se dice continua en un punto “a” si se cumplen tres condiciones:

* El límite de f(x) cuando x se aproxima a “a” existe, es decir, los límites laterales en el punto “a” coinciden.

* El valor de f(a) está definido.

* El límite de f(x) cuando x se aproxima a “a” es igual a f(a).

Cuando no se cumple alguna de las anteriores condiciones, se dice que la función es discontinua en el punto.  Por otra parte, se considera que la función es continua en un intervalo (a, b) cuando es continua en todo punto x, tal que a < x < b.

                  

Ejemplo de función continua.            La función de la figura es discontinua en el punto x = 1.

Discontinuidades evitables

Toda función que en un punto dado no cumple alguna de las condiciones necesarias para la continuidad se denomina discontinua. Cuando la discontinuidad se debe al hecho de que existe el límite de la función en el punto, pero la función no está definida para el mismo, se habla de discontinuidad evitable.

Para obtener una nueva función que sea continua también en el punto de discontinuidad evitable, se procede del modo siguiente:

• Se calcula el valor del límite de la función en el punto a.
• Se añade el punto a al dominio de definición de la función, y se le asigna el valor:

La función f (x) presenta una discontinuidad evitable en el punto x = 2. F(x) sería continua en R.

Límite lateral

Decimos que la función f(x)  tiende a L cuando x tiende a  a (o que el límite de f(x)  en a es L ) si la función  toma valores cada vez más próximos a  L cuando x se aproxima al punto a.

 Lo expresamos mediante :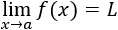 

El límite de f(x)  por la izquierda de a es L si la función  toma valores cada vez más próximos a L cuando x se aproxima al punto a por su izquierda.

Lo denotamos por.            

Análogamente, el límite de f(x)  por la derecha de a es L si la función  toma valores cada vez más próximos a L cuando x se aproxima al punto a por su derecha.

Lo denotamos por.         

MI PUNTO DE VISTA.

Hola profe, en la clase pasada vimos sobre el tema de de la continuidad que para cumplirse tienes que hacer  3 condiciones  se me hizo poco confuso pero estoy tratando de entenderle .

las clases pasadas de factorizacion y racionalizacion eso si se me esta conplicando mucho para hacer las ultimas operaciones .

Fuentes de información

https://www.resueltoos.com/blog/matematicas/estudio-de-continuidad.

https://www.hiru.eus/es/matematicas/continuidad-de-funciones.

www.fisicalab.com/apartado/continuidad-funciones

www.anep.edu.uy

VIDEOS DE YOUTUBE

https://youtu.be/pJ40TwrAZ9k?si=rdr6TCNT_qUF6Va9 

https://youtu.be/I_iy8XpHY_w?si=_BGH4LJZhVrqKGhd