Otra interpretaci贸n com煤n es que la derivada nos da la pendiente de la recta tangente a la gr谩fica de la funci贸n en ese punto. Aprende c贸mo definimos la derivada mediante l铆mites. Conoce un conjunto de reglas muy 煤tiles (como las reglas de potencia, producto y cociente) que nos ayudan a encontrar derivadas r谩pidamente.
- Es la tasa de cambio de una funci贸n en un punto espec铆fico.
- La explicaci贸n de la derivada como una funci贸n es que refleja la tasa de cambio de una variable respecto a otra.
- La interpretaci贸n geom茅trica de la derivada es la pendiente de la recta tangente a un punto de la funci贸n.
 |
| FORMULA |
 |
Apoyo gr谩fico para la definici贸n de derivada en un punto. |
Binomio
donde se enlazan dos monomios que se suman o restan (a+b) o (a-b). Todo binomio es un polinomio, pero las expresiones algebraicas pueden contar con m谩s de dos t茅rminos por lo cual existen polinomios que no son binomios, de tres, cuatro o m谩s t茅rminos.
Para averiguar las potencias de un binomio se recurre a la llamada f贸rmula del binomio de Newton, que consiste en un algoritmo donde se emplean una sucesi贸n de n煤meros combinatorios o coeficientes binomiales.
El grado de un binomio es el que corresponde a su t茅rmino de mayor grado. Los coeficientes de un monomio pueden sumarse si son semejantes entre s铆 y el resultado es un monomio, pudiendo aplicarse las propiedades conmutativa y asociativa.
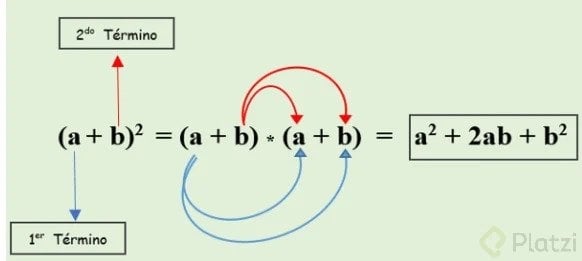
La suma de un binomio al cuadrado (a + b)2 es igual al primer t茅rmino al cuadrado sumado al producto de dos por el producto del primer t茅rmino por el segundo, a lo que se le suma el cuadrado del segundo t茅rmino: a2 + 2 • a • b + b2
La resta de un binomio al cuadrado es igual al primer t茅rmino al cuadrado, menos dos por el producto del primer t茅rmino por el segundo sumado al cuadrado del segundo t茅rmino.
Tambi茅n se habla de binomio cuando dos personas act煤an en conjunto y en forma cooperativa, potenciando sus habilidades, por ejemplo: “Juan y Mar铆a forman un binomio muy eficaz a la hora de elaborar proyectos cient铆ficos”.
HOLA PROFE buen dia,
el dia sabado en clase vimos sobre derivadas y que con la formula del dinomio tenemos que usarla para que nuestra nuestro resultado y nuestra escuasion este correcta .
profe la verdad se me esta asido dificil entender los temas anteriores y e visto videos y tambien hecho ejercicios y todo bien pero al monto que estoy en un examen o asi ya seme olvida 馃槗馃槩, pero estare dando todo de mi parte para entenderle mas y mas asta poder dominarlo .
Comentarios
Publicar un comentario