Ir al contenido principal

REGLAS DE LA DERIVACCION ALGEBRAICA.



HOLA PROFE,
Como en las clases anteriores ya aviamos visto la regla de cuatro pasos que son bastante laboriosa y tediosa  con el concepto de derivar por medio de LIMITES , tambien nos resulta demasiado engorroso tener que calcular un l铆mite cada vez que estamos resolviendo un problema. Por esta raz贸n nos ense帽o a  derivar con un proceso r谩pido y f谩cil en el los calculos de funciones de uso m谩s frecuente con las reglas  que nos permitir谩n calcular derivadas m谩s f谩cilmente y posteriormente utilizaremos el DERIVE . en este tema que vimos se me hizo un poco mas facil en la manera de derivar .

_____________________________________________________________________________________

La derivada de una funci贸n en un punto mide la rapidez con la que la funci贸n est谩 cambiando en ese punto espec铆fico. En otras palabras, representa la pendiente de la recta tangente a la curva de la funci贸n en ese punto. derivada

Es la derivada de una constante. 1. Es la derivada de una variable (cuando se deriva respecto a ella misma). 2. Es la derivada de una constante por una variable. 3. Es la derivada de una suma o resta (se pueden hacer individualmente) 4. Es la derivada de la variable elevada a una potencia. 5. Es la derivada de una funci贸n elevada a una potencia 6. Es la derivada de un producto (multiplicaci贸n). 7. Es la derivada de un cociente (divisi贸n). 8. derivada

La regla de la constante establece que si f(x)=c, donde c es una constante, entonces la derivada f′(x) es igual a cero. la regla de la constante Por lo tanto, la derivada de f(x)=5 es cero, ya que es una constante y no cambia con respecto a X. Este es un ejemplo simple de la regla de la constante en la derivaci贸n.

Establece que la derivada de x con respecto a x es igual a 1. variable respecto a s铆 misma Esto significa que la derivada de f(x)=x con respecto a x es igual a 1. En otras palabras, la tasa de cambio de x consigo mismo es constante y es 1.

Donde c es una constante. Esto significa que cuando derivas una constante multiplicada por una variable respecto a esa variable, obtienes simplemente la constante como resultado. derivada de una constante por una variable Por lo tanto, la derivada de f(x)=3x con respecto a x es simplemente 3. Esto ilustra c贸mo la constante (en este caso, 3) se mantiene igual cuando derivas con respecto a la variable.

Establece que la derivada de la suma o resta de dos funciones es igual a la suma o resta de las derivadas de esas funciones. derivada de una suma o resta Por lo tanto, la derivada de f(x)=3x con respecto a x es simplemente 3. Esto ilustra c贸mo la constante (en este caso, 3) se mantiene igual cuando derivas con respecto a la variable.

Para derivar una variable elevada a una potencia, multiplicamos la potencia original por el coeficiente y disminuimos la potencia en uno. derivada de la variable elevada a una potencia La derivada de una variable elevada a una potencia se obtiene multiplicando la potencia por el coeficiente original y disminuyendo la potencia en uno.

Se conoce como la regla de la cadena. Matem谩ticamente, si tienes una funci贸n g(x)=f(x)n, donde f(x) es una funci贸n y n es una constante, entonces la derivada g′(x) se calcula como: derivada de una funci贸n elevada a una potencia La derivada de una variable elevada a una potencia se obtiene multiplicando la potencia por el coeficiente original y disminuyendo la potencia en uno.


Regla del producto

Si f(x) y g(x) son dos funciones, considerando ambos factores, definimos la derivada de la siguiente forma:

la derivada del primero, por el segundo sin derivar, m谩s, el primero sin derivar, por la derivada del segundo

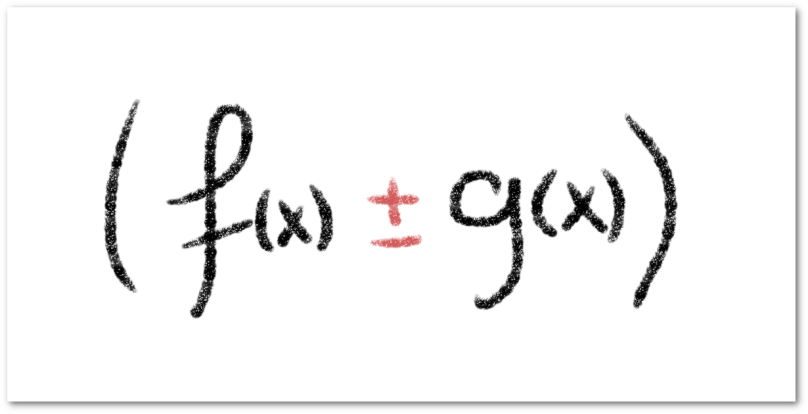
\big( f(x) \cdot g(x) \big)' = f'(x) \cdot g(x) + f(x) \cdot g'(x)





Derivada del cociente:


Si h es el cociente entre f y g, teniendo en cuenta la derivada del producto y la de una funci贸n inversa, podemos obtener de golpe la expresi贸n de la derivada del cociente considerando el producto entre f y g elevada a -1:

Derivada cociente




Regla de la cadena

La regla de la cadena es una f贸rmula que sirve para derivar funciones compuestas. La regla de la cadena establece que la derivada de una funci贸n compuesta f(g(x)) es igual a la derivada f'(g(x)) multiplicada por la derivada g'(x).


\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1pt, boxsep=1.5mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} z(x)=f\bigl(g(x)\bigr) \quad\color{orange}\bm{\longrightarrow}\quad\color{black}z'(x)=f'\bigl(g(x)\bigr)\cdot g'(x) \end{empheq}

_____________________________________________________________________________________


formulas de las derivadas.           























FUENTES DE INFORMACION :




Comentarios

Publicar un comentario

Entradas populares de este blog

MODELOS MATEMATICOS

           ¿Qu茅 es un modelo matem谩tico? Un modelo matem谩tico es una representaci贸n de un problema o una situaci贸n real utilizando el lenguaje de las matem谩ticas, como ecuaciones, funciones y f贸rmulas, para describir la relaci贸n entre sus diferentes elementos Modelo matem谩tico: Explicaci贸n sencilla Piensa en un modelo matem谩tico como si fuera el plano de una casa. El plano no es la casa real, pero es una versi贸n simplificada con s铆mbolos y n煤meros que te ayuda a entender c贸mo es, c贸mo se distribuye y c贸mo se va a construir. De la misma forma, un modelo matem谩tico «traduce» un aspecto de la realidad a las matem谩ticas para poder analizarlo y hacer predicciones. Por ejemplo, una f贸rmula tan simple como la que usar铆as para planificar un viaje en coche es un modelo matem谩tico: DISTANCIA = VELOCIDAD x TIEMPO Este modelo te permite saber la distancia que recorrer谩s (una variable) si mantienes una cierta velocidad (otra variable) durante un tiempo determinado. Los ...
Publicar un comentario
Leer m谩s

PROBABILIDAD

                                                         ¿  QUE ES UN ESTALIGRAFIA ? En probabilidad y estad铆stica, un estad铆grafo (o estad铆stico) es una medida cuantitativa calculada a partir de los datos de una muestra para describir alguna caracter铆stica de esa muestra o para estimar una caracter铆stica (par谩metro) de la poblaci贸n de la que se extrajo la muestra. Ejemplos comunes de estad铆grafos incluyen la media, la mediana, la moda y la desviaci贸n est谩ndar de una muestra.                                Son valores que tipifican una muestra y en torno de los cuales se agrupan la mayor铆a de los datos, estos se denominan estadigrafos .  Definiremos cada uno de estos : Estad铆grafos:  Valores que resumen una muestra y alrededor de los cuales se agrupa...
Publicar un comentario
Leer m谩s

APROXIMACIONES Y ERRORES

  !APROXIMACION Y ERROR POR REDONDEO¡ Entender el concepto de ERROR es importante para usar de manera efectiva los m茅todos num茅ricos. Estos m茅todos num茅ricos son el coraz贸n de la Unidad Curricular C谩lculo Num茅rico, ya que la misma gira en torno al aprendizaje de los mismos para la formulaci贸n de problemas matem谩ticos. El an谩lisis num茅rico estudia c贸mo un problema es resuelto num茅ricamente, parte de este proceso es considerar los errores que aparecen en estos c谩lculos, si son de redondeo o de otra fuente.  Aunque con la t茅cnica num茅rica se puede obtener una aproximaci贸n a la soluci贸n exacta anal铆tica, existe cierta discrepancia o error, debido a que los m茅todos num茅ricos son s贸lo una aproximaci贸n. Pocas veces, somos afortunados al disponer de la soluci贸n anal铆tica y calcular el error en forma exacta. Pero para muchos problemas de aplicaci贸n no se puede obtener una soluci贸n anal铆tica, por lo tanto no podremos calcular con exactitud los errores asociados con nuestros m茅todos num茅...
Publicar un comentario
Leer m谩s