Determinación de Máximos y mínimos de una función.
Ahora que conocemos las reglas de derivación nos encontramos en mejor posición para
continuar con las aplicaciones de la derivada. Veremos cómo afectan las derivadas la forma de la gráfica de una función y en particular cómo nos ayudan a localizar valores máximos
y mínimos de las funciones Expliquemos con exactitud qué queremos
decir con valores máximos y mínimos.
Un punto máximo absoluto es un punto en el que la función adquiere su valor máximo posible. De forma similar, un punto mínimo absoluto es un punto en el que la función adquiere su valor mínimo posible.
Los máximos o mínimos de una función son conocidos como extremos de una función, son los valores mas grandes (máximos) o mas pequeños (mínimos) que toma una función en punto situado ya sea en lo mas alto o bajo de la curva o en el dominio de la función en su totalidad.
La determinación de los valores máximos y mínimos de una función, es uno de los logros de la gran potencia que tiene el cálculo. Tomemos f(x) como una función de x. el valor de x para el cual la derivada de f(x) respecto a x es igual a cero, corresponde a los puntos de inflexión de la función f(x) donde sus valores son máximo y mínimo.
EJEMPLO : La función tiene un máximo relativo en (0, 0) y un mínimo relativo en (2, -4). que x=0 es un máximo en los puntos de su alrededor, pero no en todos, ya que, por ejemplo,
Máximos y mínimos absolutos
Los extremos absolutos son los valores de una función f más grandes (máximos) o más pequeños (mínimos) de todo el dominio.
Máximos y mínimos relativos
Los extremos relativos de una función f son los valores más grandes (máximos) o más pequeños (mínimos) de una región del dominio.
Los extremos relativos también son conocidos como extremos locales.
- La función f tiene en M un máximo relativo si f(M) es mayor que sus valores próximos a izquierda y derecha.
También se puede decir que M es un máximo relativo en su entorno si a la izquierda la función es creciente y a la derecha decreciente.
La función f tiene en m un mínimo relativo si f(m) es menor que sus valores próximos a izquierda y derecha.
Teorema de los valores extremos
Una función f(x) continua en un intervalo cerrado [a,b] siempre tiene máximo absoluto y un mínimo absoluto en dicho intervalo.
No se asegura que existan extremos absolutos si se define en un intervalo abierto.
Criterio de la Segunda Derivada
Suponga que las segundas derivadas parciales de f(x,y) existen y son continuas en un disco de centro (a,b) y suponga que fx(a,b)=0 y fy(a,b)=0 es decir (a,b) es un punto critico de f(x,y) sea:








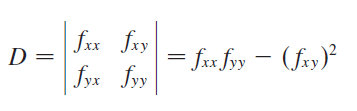



Comentarios
Publicar un comentario