Metodo de Newton Raphson

Metodo de Newton Raphson

El método de Newton-Raphson fue creado por Isaac Newton y posteriormente simplificado y popularizado por Joseph Raphson, de ahí su nombre. Newton ideó el método en 1669, mientras que Raphson publicó una versión del método en 1690 que se asemeja más a la forma moderna que se conoce hoy.

Isaac Newton: Fue quien formuló originalmente el método, aunque su descripción difería de la versión actual.
Joseph Raphson: Fue un matemático inglés que en 1690 publicó su propia versión simplificada del método, que se convirtió en la base del método moderno que se utiliza para encontrar aproximaciones de raíces de funciones.

El método de Newton-Raphson, es un método abierto y se basan en fórmulas que solamente requieren de un solo valor de inicio x o que empiecen con un par de ellos, pero que no necesariamente encierran la raíz. Éstos, algunas veces, divergen o se alejan de la raíz verdadera a medida que avanzan en el cálculo, Sin embargo cuando estos métodos abiertos convergen, en general lo hacen mucho más rápido que los métodos cerrados.

El método iterativo para sistemas de ecuaciones converge lineal mente. Como en el método de una incógnita. En fórmula de Newton-Raphson, si el valor inicial para la raíz es xi, entonces se puede trazar una tangente desde el punto [xi, f (xi)]. Por lo común, el punto donde esta tangente cruza al eje x representa una aproximación mejorada de la raíz.

No hay un criterio general de convergencia para el método de Newton-Raphson. Su convergencia depende de la naturaleza de la función y la exactitud del valor inicial. La única solución en estos casos es tener un valor inicial suficientemente cercano a la raíz. Y para algunas ocasiones ningún valor inicial no funcionara. Los buenos valores iniciales por lo común se predicen con un conocimiento del problema físico.

Formula

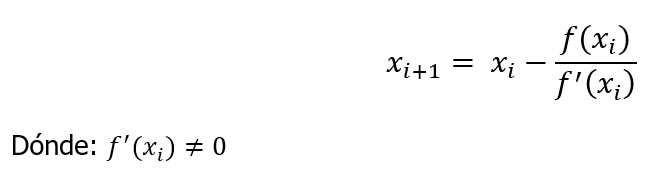Procedimiento:

Se elige un valor inicial de xi.
Se calcula f´(xi) .
Si: 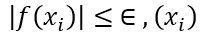es una solución estimada; en caso contrario, continuar con el paso 4.
Se calcula xi+1 a partir de la formula.
xi se iguala a xi+1 y se regresa al paso 2.

Aplicaciones:

Este método se puede aplicar en:

El desplazamiento de una estructura para una oscilación amortiguada.
En finanzas
El principio de la esfera sumergida en agua
Para resolver sistemas de ecuaciones no lineales

Fuentes:
https://www.ingenieriaquimicareviews.com/2021/07/simulacion-procesos-quimicos-newton-raphson-metodo.html
https://metododenewton.wordpress.com › 2010/04/04
https://youtu.be/9po1Lt0_4lw?si=XVOVa1q3H9v62GsR
https://youtu.be/9po1Lt0_4lw?si=XVOVa1q3H9v62GsR

https://mmerevise.co.uk › A Level Maths Revision

Comentarios

Entradas populares de este blog

MODELOS MATEMATICOS

¿Qué es un modelo matemático? Un modelo matemático es una representación de un problema o una situación real utilizando el lenguaje de las matemáticas, como ecuaciones, funciones y fórmulas, para describir la relación entre sus diferentes elementos Modelo matemático: Explicación sencilla Piensa en un modelo matemático como si fuera el plano de una casa. El plano no es la casa real, pero es una versión simplificada con símbolos y números que te ayuda a entender cómo es, cómo se distribuye y cómo se va a construir. De la misma forma, un modelo matemático «traduce» un aspecto de la realidad a las matemáticas para poder analizarlo y hacer predicciones. Por ejemplo, una fórmula tan simple como la que usarías para planificar un viaje en coche es un modelo matemático: DISTANCIA = VELOCIDAD x TIEMPO Este modelo te permite saber la distancia que recorrerás (una variable) si mantienes una cierta velocidad (otra variable) durante un tiempo determinado. Los ...

REGLAS DE LA DERIVACCION ALGEBRAICA.

HOLA PROFE, Como en las clases anteriores ya aviamos visto la regla de cuatro pasos que son bastante laboriosa y tediosa con el concepto de derivar por medio de LIMITES , tambien nos resulta demasiado engorroso tener que calcular un límite cada vez que estamos resolviendo un problema. Por esta razón nos enseño a derivar con un proceso rápido y fácil en el los calculos de funciones de uso más frecuente con las reglas que nos permitirán calcular derivadas más fácilmente y posteriormente utilizaremos el DERIVE . en este tema que vimos se me hizo un poco mas facil en la manera de derivar . _____________________________________________________________________________________ Regla del producto Si y son do s funciones, considerando ambos factores, definimos la derivada de la siguiente forma: la derivada del primero, por el segundo sin derivar, más, el primero sin derivar, por la derivada del segundo ...

PROBABILIDAD

¿ QUE ES UN ESTALIGRAFIA ? En probabilidad y estadística, un estadígrafo (o estadístico) es una medida cuantitativa calculada a partir de los datos de una muestra para describir alguna característica de esa muestra o para estimar una característica (parámetro) de la población de la que se extrajo la muestra. Ejemplos comunes de estadígrafos incluyen la media, la mediana, la moda y la desviación estándar de una muestra. Son valores que tipifican una muestra y en torno de los cuales se agrupan la mayoría de los datos, estos se denominan estadigrafos . Definiremos cada uno de estos : Estadígrafos: Valores que resumen una muestra y alrededor de los cuales se agrupa...

HEIDYBLOGS🤍

Buscar este blog